M.C. Escher

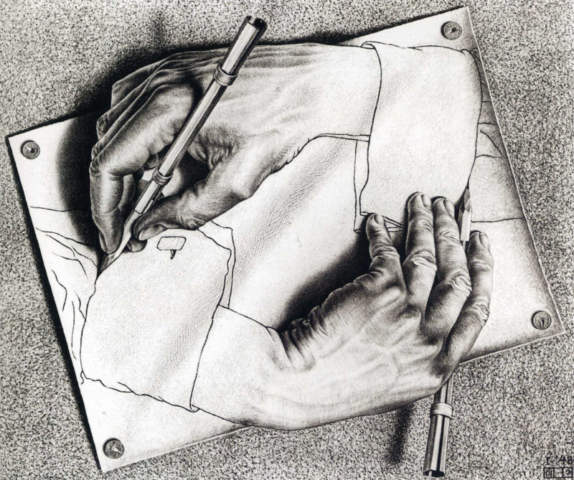
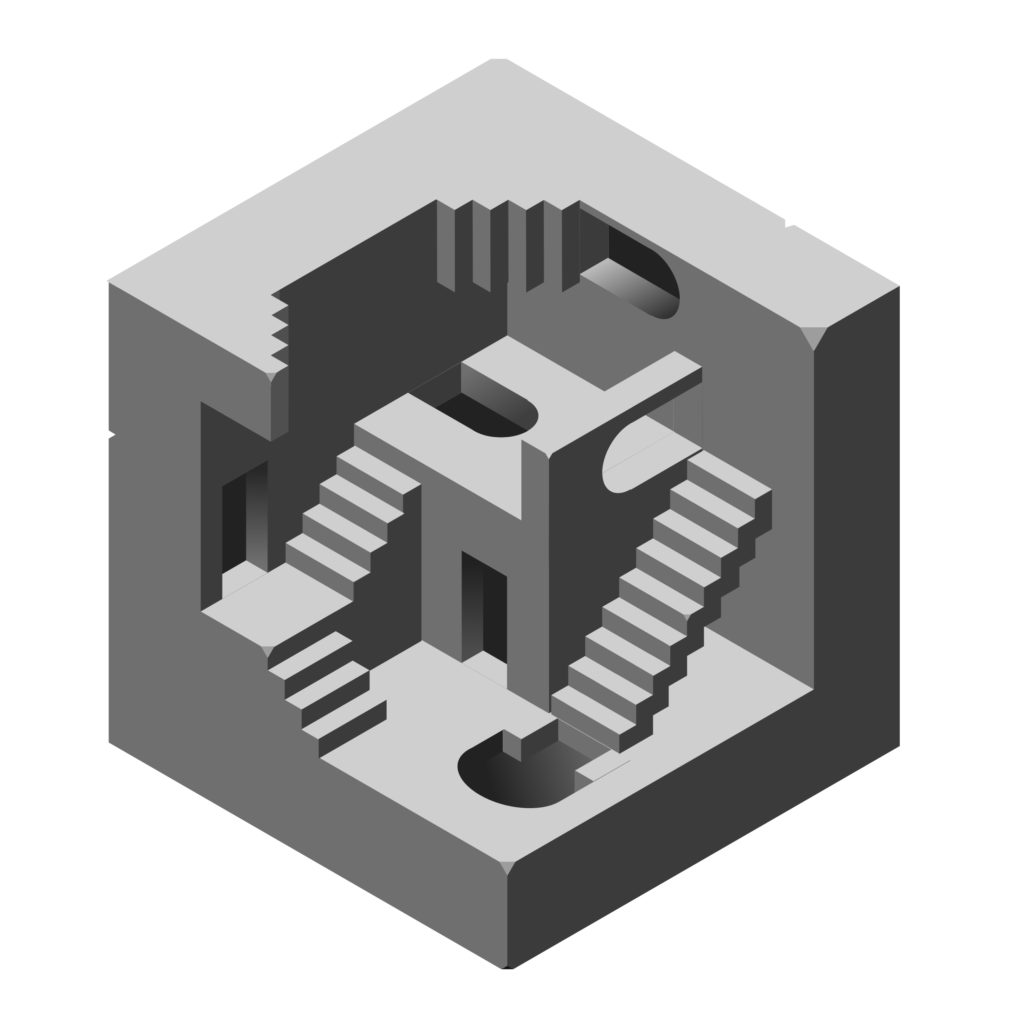
Escher ou comment déformer la réalité

Introduction 

Il y a des artistes qui ont véritablement marqué le monde , qui ont créer des images qui ont redéfini les règles … Celui qui m’intéresse aujourd’hui est de ceux là ! Entre art et mathématique la frontière est mince, et lui , on peut dire qu’il ne l’a pas seulement franchi mais l’a carrément étiré dans tous les sens … Tout d’abord je voudrais profiter de cet élan ou je te parle de perspective ( tu peux retrouver le premier volet de cette série ici ) pour te présenter un de mes artistes préférés M.c. Escher !

De même que pour l’article que j’avais rédigé sur le cubisme je ne vais pas me contenter de simplement en parler et te raconter des choses qui ont déjà été dites pleins de fois sur le web… Je voudrais surtout tenter de comprendre une des ses oeuvres et adapter le style à une illustration isométrique

Histoire d’ Escher

Tout d’abord Maurits Cornelis Escher est un artiste néerlandais connu pour ses oeuvres défiants toutes les lois de la physique … Il est né en 1898 et est décédé en 1972 et il faut souligner qu’ il a réalisé plus de 2000 estampes , dessins , lithographies et gravures sur bois très souvent inspirées des mathématiques !

 « Mauk » de son surnom est connu pour ses formes impossibles , ses imbrications et ses déformations 

Il à étudié l’architecture et les arts visuels mais n’était pas très bon à l’école… Cependant c’est au cours de l’un de se voyages en Espagne qu’il à eu le déclic en découvrant les ornementations mathématiques complexes de l’Alhambra , un château Maure situé à Grenade . 

Il faut savoir qu’il à vécu un moment en Belgique , à Uccle de 1937 à 1941 . Lui et sa famille on du retourner aux Pays Bas à cause de la 2eme Guerre mondiale 

Description de son boulot 

Escher à été très influencé par les mathématiques et notamment par son amis le mathématicien Roger Penrose… En fait il à même donné son nom à une de ses oeuvres les plus connues , le triangle de Penrose. En fait il a passé sa carrière à déformer la réalité , les perspectives et la gravité ! 

C’est pour moi l’artiste qui maitrise le mieux les règles de la perspective et donc la construction d’une scène 

Son travail est encore aujourd’hui le plus pointu en la matière et bon nombre de mathématiciens continuent toujours d’essayer de percer ses secrets… En fait il à réussi à marquer de manière très forte des générations d’artistes ( dont moi ) dans tous les domaines créatifs 

Un des éléments qui rends sont boulot si marquant est que ses oeuvres rappellent énormément le monde du rêve … Il disait d’ailleurs souvent en parlant de son travail : «  Tout cela n’est rien comparé à ce que je vois dans ma tête ! »

Quelques unes des œuvres d’Escher

Tu peux aussi aller jeter un oeil sur son site officiel qui est géré par la M.C.Escher Foundation et la M.C.Escher Company.

Les références à Escher dans la pop culture

Son univers unique à inspiré une foule d’artistes de toutes disciplines , en voici donc quelques uns des plus connu !

Dans le cinéma : 

Labirinth (1986 ) Jim Henson > https://www.youtube.com/watch?v=k1Z2pk5J9Ng&feature=emb_title

Harry Potter à l’école des sorciers (2001) Chris Colombus > https://www.youtube.com/watch?v=9aZxsOZ50y4&feature=emb_title

Inception (2010) Christopher Nolan > https://www.youtube.com/watch?v=evPzM7JeQQg&feature=emb_title

Dans la musique : 

Incubus , Drive , le clip montre deux mains qui se dessinent elles même > https://www.youtube.com/watch?v=fgT9zGkiLig&feature=emb_title

DaftPunk, around the world , le clip par gondry est inspiré du miroir homme-singe > https://www.youtube.com/watch?v=LKYPYj2XX80&feature=emb_title

Relativity 

Alors … pour aller plus loin dans l’analyse on va reproduire une des œuvres les plus importantes de ce génie ! J’ai nommé Relativity, une gravure qui contient 3 axes de gravités et représente un espace sur plusieurs niveaux séparés par des escaliers . 

Cet espace est peuplé de personnages qui vivent leur vie et cohabitent sur trois axes différents ! Ce qui est un mur pour certains est le sol pour d’autres … Certains personnages empruntent le même escalier mais sur deux plans différents ! Tout comme la végétation et les objets qui se divisent sur les différents axes de gravités . 

• 

• 

• 

• 

• 

• 

Quand on parcourt l’oeuvre du regard , on peut voir que ce monde semble être idyllique mais pourtant on se sent très vite gagné par un sentiment de malaise et d’inquiétude… C’est dû au fait , entre autres , que cette représentation n’est pas sans rappeler le monde du rêve mais aussi et surtout celui des cauchemars ! 

C’est une des caractéristiques du travail d’Escher … Toutes ses oeuvres obéissent aux même lois avec des distances qui s’étirent , des perspectives impossibles ou des métamorphoses … Son escalier sans fin à d’ailleurs servi à illustrer le contexte de l’architecture des rêves dans le film Inception 

Reproduction de certaines des œuvres d’ Escher et explications 

Au départ , je voulais juste reproduire Relativity et l’adapter à la perspective Isométrique ! Pourquoi isométrique ? Et bien parce que je suis en train de bosser sur une série sur la perspective ( tu peux d’ailleurs retrouver le premier volet ici ) et que ça me semblait être une bonne base pour ça …

Bref , j’ai réalisé une illustration inspirée de Relativity… Au moment de commencer je me suis dit que ça pourrait être sympa de faire rentrer la scène dans un hexagone parce que ça colle super bien avec les angles de la perspective isométrique ! 

Quand j’ai fini mon oeuvre , j’ai directement eu envie d’enchainer sur l’escalier sans fin puis sur le cube de Penrose . Enfin j’ai eu envie de m’essayer au triangle de Penrose … Et j’ai fais tout ça en isométrie … Et tout rentre dans des hexagones ! Sauf le triangle ( vu que c’est un triangle ) … MAIS j’ai quand même utilisé un hexagone comme base de travail . 

Voyons ça ensemble : 

Relativity … 

Comme Escher avec son oeuvre,  j’ai donc fais se côtoyer 3 gravités dans la même scène . J’ai hésité à tenter le coup avec 6 gravités mais ça aurait fait un peu chargé pour petite illu comme celle là .

En premier lieu la question que je me suis posé était de savoir si Escher s’était amusé à changer des objets convexes en objets concaves comme sur l’illustration ci-dessous ( celle de droite ) 

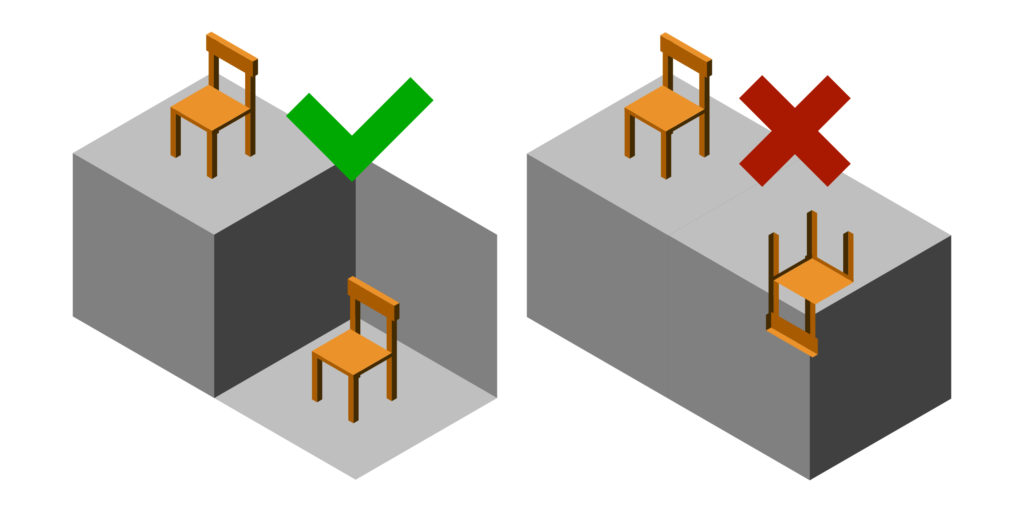
Donc en regardant en détails l’oeuvre je n’ai eu aucun mal à me rendre compte que … Et bin NON ! En fait tout est dans la même réalité si on ne tient pas compte des 3 gravités différentes ! Alors j’entends par là que si un personnage peut se balader dans la scène et diriger le gravité, il n’aura pas à changer de perspective pour passer d’un endroit à l’autre.

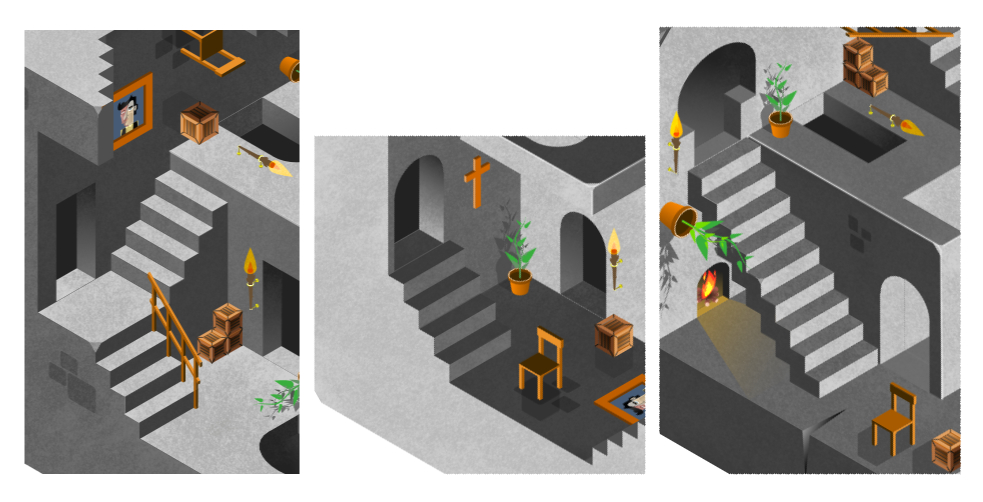
Finalement après quelques expérimentations dans le genre , je me suis lancé dans la création de ma scène : 

J’ai d’abord créé un espace isométrique qui rentrait dans un hexagone … Puis je suis parti d’un volume simple auquel j’ai ajouté des escaliers , un pour chaque gravité. Le tout en nuance de gris , pour favoriser le contraste et faire quelques choses de neutre . C’est plus simple quand on expérimente ! 

• 

• 

Ensuite j’ai créé des ouvertures et des portes puis des éléments de décorations dans tous les sens ! Les objets étant eux en couleur ça crée un chouette dosage avec les gris des murs et escaliers ! ça rend la scène plus claire et nette ! 

Après tout ça je n’avais plus qu’à ajouter les textures et les petits détails qui rendent tout plus réaliste pour obtenir ceci ! 

Envie de plus …

Comme je te le disais plus haut , ça m’a donné envie d’aller plus loin dans les mystères d’Escher . J’ai voulu en comprendre d’avantage sur ses concepts de déformations. Je me suis donc amusé à reproduire ( pour mieux comprendre ) d’autres de ses oeuvres … 

J’avais toujours super envie de réaliser ça en perspective isométrique et toujours dans des hexagone bien évidement ! 

L’escalier sans fin …

D’abord la première étape à été de tracer un hexagone composé de trois losanges ( avec l’aide de la grille isométrique d’Affinity Designer ) avec la face horizontale vers le haut … Ainsi, c’est sur cette face supérieur que l’escalier allait se poser ! 

J’ai du faire plusieurs tentatives avant d’obtenir un « presque » escalier qui fonctionne ! Enfin en théorie car même si la première marche correspondait à la dernière il avait l’air tout tordu ! 

Finalement après quelques minutes à chipoter , à redescendre certains éléments et à en remonter d’autres … Ainsi, millimètre par millimètre , j’ai fini par avoir quelque chose de cohérent à l’oeil … Enfin il ne restait plus qu’à y ajouter des ombrages et le tour était joué 

Pour conclure l’idée pour ce concept est que les marches de l’escalier sont en dents de scie , comme sur l’illustration ci-dessous . 

Triangle de Penrose et cube de Necker … 

Alors ces deux là son super important pour mieux comprendre l’ensemble de la vision d’Escher … Par ailleurs c’est plus des exercices de style que des oeuvres à proprement parlé ! Je t’invite à les tester avant tout pour te familiariser avec le concept de formes impossibles !

J’ai commencé par le cube , je savais qu’il rentrerait dans un hexagone mais je ne savais pas ce que ça donnerait en perspective isométrique . Donc pour bien comprendre le truc j’ai commencé par crée un cube correcte … Dans les règle de l’art ! Voici le résumé du process :

Puis une fois mon cube visuellement correct fini , je suis passé au cube version Escher ! Comme tu peux le voir j’ai fais exactement pareil que pour le précédent … L’astuce se situe à l’étape 4 et c’est à partir de là que tu peux voir la légère différence qui perturbe tout !

Tout d’abord c’était pas terrible … En fait c’était tout plat et pas très clair ! Puis c’est après avoir ombré un peu que ça a commencé à ressortir . Dans ce genre de job , en perspective isométrique en tous cas , je me suis rendu compte de l’importance de l’ombrage pour que l’illusion prenne tout son sens …

Par contre je ne pouvais pas faire le cube et ne pas faire le triangle. Bon là pour le coup ça a été plus vite quand même … Pour jouer le jeu je l’ai fais rentrer dans un hexagone aussi et j’ai utilisé un triangle qui était parallèle sur 3 cotes … 

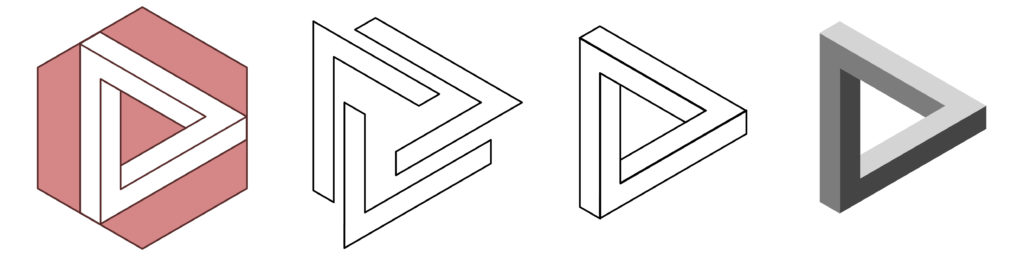
Enfin quand j’ai défini une partie , je n’avais plus qu’à la reproduire et la faire pivoter de 60 degrés 3 fois 

Puis à ombrer parce que je me suis rendu compte avec les précédents que c’est super important pour la lisibilité de ce style de job ! 

Conclusion

Alors voila , j’espère que cet article t’as plu et qu’il t’aura donné l’envie d’en apprendre un peu plus sur M.C. Escher ! C’est assez difficile de résumer tout ce j’avais à dire sur son boulot sans que ça prenne trop de place alors j’ai du faire des choix … sélectionner ce qui me semblait important et je pense que j’ai dû oublier certaines choses ! Alors si quelques choses te vient en tête n’hésites pas à m’écrire pour me dire ça ^^

Par ailleurs n’oublie pas de t’inscrire à ma Newsletter pour être tenu au courant en premier des nouveaux articles qui paraitront sur ce blog